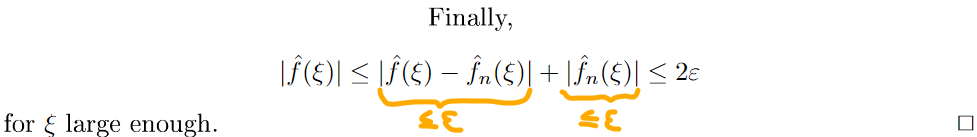Lemme de Riemann-Lebesgue - Math'φsics

Lemme de Riemann-Lebesgue

Formulaire de report
Problème d'affichage Contenu de la note peu pertinent
Lemme de Riemann-Lebesgue :
\(f\in L^1({\Bbb R})\)

\(f\in \mathcal C_c^k({\Bbb R})\) avec \(f^{(k)}\in L^1({\Bbb R})\)

$$\Huge\iff$$

$$\lvert \hat f(\xi)\rvert\leqslant\frac{\lVert f^{(k)}\rVert_2}{\lvert\xi\rvert^k}$$
Démontrer :

On procède par IPPs multiples.

Démontrer \(ii)\) :

On approche \(f\in L^1\) par une suite de fonctions \(\mathcal C^\infty\) pour \(\lVert\cdot\rVert_1\).

Alors la norme de la différence est \(\leqslant\varepsilon\) pour \(n\) assez grand, et donc \(\lVert \hat f_n-\hat f\rVert_\infty\leqslant\varepsilon\).

Le point \((i)\) nous dit que \(\lvert\hat f_n(\xi)\rvert\leqslant\varepsilon\) pour \(\xi\) assez grand.

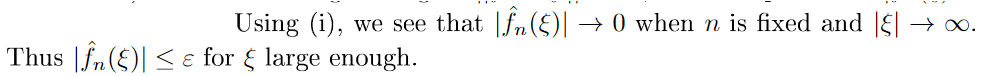
Une inégalité triangulaire forcée nous permet de conclure en utilisant ces deux majorations.
Rétroliens :
- Convergence uniforme